PBR论文简读：A Practical Model for Subsurface Light Transport

导语

离线环境下进行真实感渲染的时候，会有各种散射材质，比如人类皮肤、硅胶等。从外观上看，这类材质的通性在于都有一种“透光”的感觉，简单的使用brdf创造出来的材质往往显得很生硬，因此Jensen'01的这篇论文给出了一个实际的次表面散射（subsurface scattering）bxdf来实现这种材质。

理论

BRDF理论假设材质光的进入和离开的起、终点一致，本质上是对BSSRDF的一种近似\(x_o = x_i\)，并且给出的积分公式也是简单地在半球面上进行积分，BSSRDF则考虑的是出、入射点不同时，对于区域\(A\)内所有入射光线的radiance的半球面积分：

\[L_o = \int_A\int_{2\pi}S\cdot L_i\cdot (\vec n\cdot \vec {\omega_i})d\omega_i dA(x_i)\]

我们需要的就是文章给出的BSSRDF：\(S\)项，这里Jensen'01的论文将次表面散射的BSSRDF拆解成了Diffusion Approximation和Single Scattering两个term求和。前者基于的是：通过观察，发现高度散射的介质的光线分布有着各项同性的特征（即使入射光和相位函数是高度各向异性的），后者论文中并没有给出一个拆分的理由，而是从前人的论文中得到的BRDF扩展成为了BBSSRDF，并且后者当且仅当出、入射光的折射发生相交时才会出现，个人理解是对于diffuse的一个specular补偿。

推导

在介质中，光线的传播被我们使用辐射传播方程所描述：

\[(\vec{\omega} \cdot \vec{\nabla}) L(x, \vec{\omega})=-\sigma_{t} L(x, \vec{\omega})+\sigma_{s} \int_{4 \pi} p\left(\vec{\omega}, \vec{\omega}^{\prime}\right) L\left(x, \vec{\omega}^{\prime}\right) d \omega^{\prime}+Q(x, \vec{\omega})\]

我们分别使用三个参数：吸收系数\(\sigma_\alpha\), 散射系数\(\sigma_s\)（这两者的和定义为消散系数\(\sigma_t\)）和相位函数\(p(\vec w, \vec w')\)来描述介质的属性，其中相位函数可以看作是描述在介质中一点的光线散射的角度分布^[1]的函数，同时文章假设这个函数已经normalize了（对于整个球面积分为1）。紧接着定义了平均余弦函数\(g\)用来描述相位函数的性质\(g=\int_{4 \pi}\left(\vec{\omega} \cdot \vec{\omega}^{\prime}\right) p\left(\vec{\omega} \cdot \vec{\omega}^{\prime}\right) d \omega^{\prime}\)：大于0说明散射大部分是前向的，小于0则是反向的，等于零说明在球面上均匀分布（各向同性）。对于一个理想的无穷小光束，radiance根据传播距离\(s\)的衰减定义为指数级的：\(L_{r i}\left(x_{i}+s \vec{\omega}_{i}, \vec{\omega}_{i}\right)=e^{-\sigma_{t} s} L_{i}\left(x_{i}, \vec{\omega}_{i}\right)\)。这样，一阶的散射就可以被作为次级的体积光源使用，可以得出一个点在\(x\)处接收到周围某个点发射的irradiance：\(Q(x, \vec{\omega})=\sigma_{s} \int_{4 \pi} p\left(\vec{\omega}^{\prime}, \vec{\omega}\right) L_{r i}\left(x, \vec{\omega}^{\prime}\right) d \omega^{\prime}\)。接下来就可以对\(x\)点的辐射传播方程的散射参数\(\omega'\)进行积分，获得周围所有光对\(x\)点的影响，将两个irradiance，\(\phi(x)\)和\(\vec E(x)\)联系了起来：

\[\vec{\nabla} \cdot \vec{E}(x)=-\sigma_{a} \phi(x)+Q_{0}(x)\]

这里引入的零阶源\(Q_{0}(x)=\int_{A_{\pi}} Q(x, \vec{\omega}) d \omega\)就是前文提到的次级光源，同时将更高阶的源1定义为\(\vec{Q}_{1}(x)=\int_{4 \pi} Q(x, \vec{\omega}) \vec{\omega} d \omega\)。

Diffusion Approximation

上一节说到，diffusion被看作是各向同性的，论文中就直接利用这个特性把radiance展开成了radiant fluence和vector irrandiance和（这两个本质上都是irradiance），除以了球体单位角的总和\(4\pi\)即是\(Le\)（原文里面说这两个的常数系数是由fluence和vector irradiance的定义决定的）：

\[L(x, \vec{\omega})=\frac{1}{4 \pi} \phi(x)+\frac{3}{4 \pi} \vec{\omega} \cdot \vec{E}(x) \tag{1}\]

将这个式子代入辐射传播方程，类似的，对\(\omega\)进行积分，得到的结果式：\(\vec{\nabla} \phi(x)=-3 \sigma_{t}^{\prime} \vec{E}(x)+\vec{Q}_{1}(x)\)，其中\(\sigma_{t}^{\prime}=\sigma_{s}^{\prime}+\sigma_{a} \text { where } \sigma_{s}^{\prime}=\sigma_{s}(1-g)\)，然后将上式带入上上个等式，得到经典的diffusion方程：

\[D \nabla^{2} \phi(x)=\sigma_{a} \phi(x)-Q_{0}(x)+3 D \vec{\nabla} \cdot \vec{Q}_{1}(x)\]

在一个无限大的介质里的各项同性点光源，上式\(x\)点的irradiance有一个简单的解如下：

\[\phi(x)=\frac{\Phi}{4 \pi D} \frac{e^{-\sigma_{t r} r(x)}}{r(x)}\]

当考虑传输介质是处于有限区域的时候，就需要考虑边界区域（出射）的情况，这里论文考虑边界只有出射的情况，也就是入射的flux为0：\(\int_{2 \pi_{-}} L\left(x_{s}, \vec{\omega}\right)\left(\vec{\omega} \cdot \vec{n}\left(x_{s}\right)\right) d \omega=0\)（法线向外，但是在内部积分），使用公式(1)展开有：

\[\phi\left(x_{s}\right)-2 D(\vec{n} \cdot \vec{\nabla}) \phi\left(x_{s}\right)=0 \tag{3}\]

但是上面的公式只考虑了surface两边IOR相等的情况，对于两边不等的情况，在表面处会发生反射，根据菲涅尔公式可以计算出平均的菲涅尔漫反射系数\(F_{dr}\)，具体方法就是对菲涅尔系数与视线、法线的夹角余弦做积分。可以用菲涅尔公式做一个解析的解，但是论文里面选择了一个基于多项式的近似：

\[F_{d r}=-\frac{1.440}{\eta^{2}}+\frac{0.710}{\eta}+0.668+0.0636 \eta\]

根据前文的净通量为0，同样的有：

\[\phi\left(x_{s}\right)-2 D(\vec{n} \cdot \vec{\nabla}) \phi\left(x_{s}\right)=F_{d r}\left[\phi\left(x_{s}\right)+2 D(\vec{n} \cdot \vec{\nabla}) \phi\left(x_{s}\right)\right]\]

化简：

\[\phi\left(x_{s}\right)-2 A D(\vec{n} \cdot \vec{\nabla}) \phi\left(x_{s}\right)=0\tag{4}\]

实际上观察这个公式和(3)的区别也仅仅在于多了一个平均漫射菲涅尔系数相关的\(A\)。这样我们就可以根据边界的值，通过出射的radiance（\(\vec n \cdot \vec E(x_s)\)等于表面的通量梯度）除以入射的flux计算出BSSRDF diffusion approximation了：

\[R_{d}(r)=-D \frac{(\vec{n} \cdot \vec{\nabla} \phi)\left(x_{s}\right)}{d \Phi_{i}\left(x_{i}\right)}\]

但是有限介质的辐射方程没有精确的解析解，为了简化模型，论文引用了“双极子”的方法模拟体积光源分布，对于次级体积光源，引入了两个点光源：

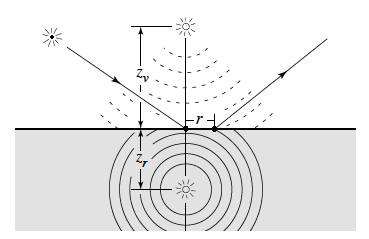
其中正光源在surface下，负光源在surface上，用来模拟光的衰减效应，两者总体的fluence满足：

\[\phi(x)=\frac{\Phi}{4 \pi D}\left(\frac{e^{-\sigma_{t r} d_{r}}}{d_{r}}-\frac{e^{-\sigma_{t r} d_{v}}}{d_{v}}\right)\]

这样，在有限介质下的边界条件也得到了，紧接着就可以带入之前的公式求出\(R_d(r)\)了

\[\begin{aligned} R_{d}(r) &=-D \frac{\left(\vec{n} \cdot \vec{\nabla} \phi\left(x_{s}\right)\right)}{d \Phi_{i}} \\ &=\frac{\alpha^{\prime}}{4 \pi}\left[\left(\sigma_{t r} d_{r}+1\right) \frac{e^{-\sigma_{t r} d_{r}}}{\sigma_{t}^{\prime} d_{r}^{3}}+z_{v}\left(\sigma_{t r} d_{v}+1\right) \frac{e^{-\sigma_{t r} d_{v}}}{\sigma_{t}^{\prime} d_{v}^{3}}\right] \end{aligned}\]

Update 2022-5-12 在实现本论文算法的时候发现这个\(R_d(r)\)的式子是有问题的，第二行中括号前后两个式子的量纲是不一样的（后面的式子多了一个\(z_v\)，会导致结果与实际产生10的指数级别的误差，正确的公式应该参照d'Eon的A better dipole中给出的公式（看了这么多实现竟然没有人指出这个问题，有点匪夷所思了））。

可以看出来，\(R_d\)项实际上是只与散射材料本身和双极子与表面距离相关的函数（非严格意义上的反比例，这样就给出了一个很好的性质，让我们在做BSSRDF积分的时候不需要完整地考虑整个surface，而是主要对临近的表面积分即可），进而可以求出BSSRDF中的diffusion term：

\[S_{d}\left(x_{i}, \vec{\omega}_{i} ; x_{o}, \vec{\omega}_{o}\right)=\frac{1}{\pi} F_{t}\left(\eta, \vec{\omega}_{i}\right) R_{d}\left(\left\|x_{i}-x_{o}\right\|\right) F_{t}\left(\eta, \vec{\omega}_{o}\right)\]

这一项主要是代表了光线在介质中多次散射产生的衰减。

Single Scattering

论文中还专门将一次散射拆成了一个单独的项\(S^{(1)}\)提了出来，这里个人暂时无法理解这么做的理论依据，只能理解为单次散射无法看作各向同性的新光源，而是作为一个specular项存在：

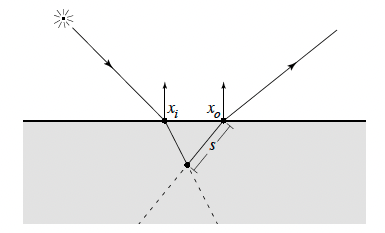
\[\begin{aligned} L_{o}^{(1)}\left(x_{o}, \vec{\omega}_{o}\right) &=\sigma_{s}\left(x_{o}\right) \int_{2 \pi} F p\left(\vec{\omega}_{i}^{\prime} \cdot \vec{\omega}_{o}^{\prime}\right) \int_{0}^{\infty} e^{-\sigma_{t c^{s}}} L_{i}\left(x_{i}, \vec{\omega}_{i}\right) d s d \vec{\omega}_{i} \\ &=\int_{A} \int_{2 \pi} S^{(1)}\left(x_{i}, \vec{\omega}_{i} ; x_{o}, \vec{\omega}_{o}\right) L_{i}\left(x_{i}, \vec{\omega}_{i}\right)\left(\vec{n} \cdot \vec{\omega}_{i}\right) d \omega_{i} d A\left(x_{i}\right) \end{aligned}\]

论文认为单次散射的出射radiance \(L_o\)等于对折射路径\(s\)上的入射radiance进行积分（第一行的内部积分），再对入射的半球面立体角进行积分，总体上也就等价于固定了\(x_o\)，再对入射的立体角和单位入射面积进行二重积分，便可以得到\(S^{(1)}\)的隐式表达。

论文里还指出了diffusion term和single scattering有着不同的平均出射距离，并且两者的距离尺度有着很大的差别，对于有效消散系数\(\sigma_{tr}\)远远小于消散系数\(\sigma_t\)，single scattering随着\(x_o\)增加而衰减的情况会远明显于diffusion。

BRDF近似

完成上面两项的推导之后，论文提出了使用BRDF模拟BSSRDF的做法：假设surface上受到的光照是均匀的，这样就可以通过对于整个surface积分来实现计算（\(r\)从0积分到正无穷），对于single scattering也是同样的，就可以得到近似的BRDF：

\[ f_{r}\left(x, \vec{\omega}_{i}, \vec{\omega}_{o}\right)=f_{r}^{(1)}\left(x, \vec{\omega}_{i}, \vec{\omega}_{o}\right)+F \frac{R_{d}}{\pi}\]

对于不透明，消散系数很大的材质（使得平均自由路径很短）来说，这个方法可以较好地模拟出BSSRDF（实际积分的权重多数集中于入射、反射点）。

BSSRDF实现

相较于BRDF，虽然我们已经简化了BSSRDF原本要求的入射区域A的积分而变成了在入射的位置进行多次采样，论文提出使用类似于分布式光线追踪的思路，在一个shadow ray的两端进行多次采样，并且针对single scattering和diffusion两项进行不同的采样。其中diffusion采样直接使用蒙特卡洛方法根据离出射点的距离，使用\(\sigma_{t r} e^{-\sigma_{t r} d}\)的权重进行采样。对于single scattering，由于入射和出射的折射光必须相交，论文对其进行了重组参数处理。

对于任意的几何表面，为了避免高度曲折情况导致的artifact，论文认为应该始终选择将双极子放置在最小距离\(1/\sigma'_t\)处，这样可以处理在边界处出现的奇点问题。同时，如果物体表面有纹理材质，那么论文将纹理近似为仅仅覆盖在物体的表面，因此内部的体积光散射将不会收到纹理的variance造成的影响。