PBR读书笔记四：Sampling Theory

对图像的描绘，本质上是场景重建(reconstruction)与信号处理(signal processing)，简单来说就是用离散的采样（像素点）来对连续的真实世界进行重建，那么就涉及到采样(sampling)的问题了。

傅立叶分析

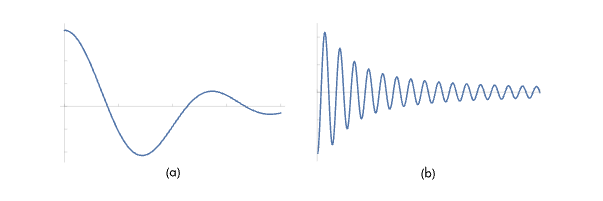
傅立叶分析可以用来评估重建函数的质量，同时其被用来在频域上分析不同频率的函数，通常来说，高频率的函数变换的较为频繁、较快；低频率的函数变化的较缓慢。如下是两个函数图像：

与之对应的，是其在频域上的函数图像：

即运用傅立叶变换：

\[F(\omega)=\int^\infty_{-\infty}f(x)\exp{(-\text{i}2\pi \omega x)}\text{d}x\]

傅立叶变换具有对称性，即函数对应的频域函数，对这个频域函数再做一次傅立叶分析得到的函数是原函数。同时，傅立叶变换中还有一个重要特性，两个函数的点积结果进行傅立叶变换得到的函数等于两个函数进行傅立叶变换之后的卷积：

\[\text{F}\{f(x)g(x)\} = F(\omega)\circledast G(\omega)\]

反走样

走样分为两种：采样瑕疵造成的前走样和重建造成的后走样。

非均匀采样

众所周知的，在GAMES202的阴影作业里提供了两种采样方法： - uniform disk sampling - poisson disk sampling

具体理论可以参考wiki-非均匀采样。在pbrt中认为虽然非均匀采样和均匀采样均无法完好地复原信号，但是非均匀的采样可以将规律性的走样转化为噪声，而对于人类的视觉系统，噪声比走样更容易被忽略。

自适应采样

理论上来说，频率越高的地方需要的采样率越高，于是可以通过增大那些发生剧变的区域采样率来达到自适应的采样。

预滤波

顾名思义，在采样之前对原始信号进行滤波，这样防止出现无法被良好采样的超高频信号。比较常用的方法就是通过一个卷积，如：

\[f(x)\circledast \text{sinc}(2\omega_s x)\]

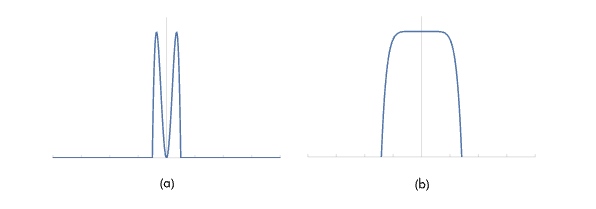
使用了一个sinc的滤波器，消除难以采样的高频信息：

sinc滤波器

图像重建

采样的结果最后是用来进行图像的重建的，这里就会遇到之前提到的后走样问题，一个典型的box filter的结果如下图

使用箱型过滤器的结果

可以选择的滤波器有很多，pbr中定义了滤波器的基础属性radius，如下图：

滤波器参数

radius是所有滤波器共有的属性，所有的滤波器也都继承自基类：

class Filter {
public:
  virtual ~Filter();
  Filter(const Vector2f &radius)
      : radius(radius),
        invRadius(Vector2f(1 / radius.x, 1 / radius.y)) { }
  virtual Float Evaluate(const Point2f &p) const = 0;
  const Vector2f radius, invRadius;
};

Box Filter

箱型滤波器是最为简单的一种滤波器，但是问题也很明显：高频率样本会发生泄漏的现象，这就是后走样形成的重要原因。这种泄漏的现象不仅仅会发生在采样率低于奈奎斯特极限的时候，在函数频率接近甚至超过奈奎斯特极限的时候同样会发生。

Triangle Filter

性质与箱型过滤器类似，略

Gaussian Filter

pbrt中对其评价为：

The Gaussian does tend to cause slight blurring of the final image compared to some of the other filters, but this blurring can actually help mask any remaining aliasing in the image.

也就是说高斯滤波器可以为图像带来有益的模糊以掩饰走样。一维高斯滤波器函数为：

\[f(x) = \exp{(-\alpha x^2)} - \exp{(-\alpha r^2)}\]

其中第二项的目的是为了保证高斯函数最后能落至0，而不是一个陡峭的剧变。二维的高斯函数则是简单的两个一维高斯函数的乘积。

Mitchell Filter

暂略